Luas & Keliling Lingkaran: Rumus Mudah, Cepat Ingat!

Ilustrasi(Dok Ist)

LINGKARAN, sebuah bangun datar yang familiar dalam kehidupan sehari-hari, menyimpan misteri matematika yang menarik untuk diungkap. Bentuknya yang sempurna, tanpa sudut dan sisi, menjadikannya objek studi yang unik dan relevan. Memahami konsep luas dan keliling lingkaran bukan hanya sekadar menghafal rumus, tetapi juga membuka wawasan tentang bagaimana matematika diterapkan dalam berbagai aspek kehidupan.

Memahami Konsep Dasar Lingkaran

Sebelum melangkah lebih jauh ke dalam perhitungan luas dan keliling, penting untuk memahami elemen-elemen dasar yang membentuk sebuah lingkaran. Elemen-elemen ini adalah kunci untuk memahami rumus dan aplikasinya. Pertama, terdapat titik pusat, yaitu titik yang berada tepat di tengah lingkaran dan menjadi acuan untuk semua pengukuran. Kemudian, ada jari-jari (r), yaitu jarak dari titik pusat ke titik mana pun pada garis lingkaran. Jari-jari selalu memiliki panjang yang sama, tidak peduli di mana pun titik tersebut berada pada lingkaran. Selanjutnya, terdapat diameter (d), yaitu garis lurus yang melewati titik pusat dan menghubungkan dua titik pada garis lingkaran. Diameter selalu dua kali panjang jari-jari (d = 2r). Terakhir, ada keliling lingkaran, yaitu panjang garis yang membentuk lingkaran itu sendiri. Keliling ini juga sering disebut sebagai circumference dalam bahasa Inggris.

Selain elemen-elemen dasar tersebut, terdapat juga konsep busur dan juring. Busur adalah sebagian dari keliling lingkaran yang dibatasi oleh dua titik pada lingkaran. Sedangkan juring adalah daerah di dalam lingkaran yang dibatasi oleh dua jari-jari dan busur yang menghubungkan kedua jari-jari tersebut. Pemahaman tentang busur dan juring penting dalam perhitungan luas sektor lingkaran dan panjang busur.

Rumus Luas Lingkaran: πr²

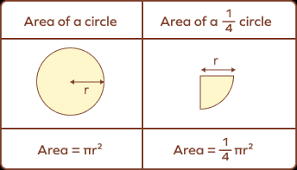
Luas lingkaran adalah area yang berada di dalam garis lingkaran. Rumus untuk menghitung luas lingkaran adalah πr², di mana π (pi) adalah konstanta matematika yang nilainya mendekati 3.14159, dan r adalah jari-jari lingkaran. Rumus ini menunjukkan bahwa luas lingkaran berbanding lurus dengan kuadrat jari-jarinya. Artinya, jika jari-jari lingkaran diperbesar dua kali lipat, maka luasnya akan menjadi empat kali lipat.

Untuk memahami asal-usul rumus ini, kita bisa membayangkan lingkaran dibagi menjadi banyak sekali juring-juring kecil. Jika juring-juring ini disusun ulang menjadi bentuk yang menyerupai persegi panjang, maka panjang persegi panjang tersebut akan mendekati setengah dari keliling lingkaran (πr), dan lebarnya akan mendekati jari-jari lingkaran (r). Dengan demikian, luas persegi panjang tersebut adalah πr r = πr², yang juga merupakan luas lingkaran.

Contoh penggunaan rumus: Jika sebuah lingkaran memiliki jari-jari 5 cm, maka luasnya adalah π 5² = π 25 ≈ 78.54 cm². Penting untuk diingat bahwa satuan luas selalu dalam bentuk kuadrat (cm², m², dll.).

Rumus Keliling Lingkaran: 2πr atau πd

Keliling lingkaran adalah panjang garis yang membentuk lingkaran. Ada dua rumus yang dapat digunakan untuk menghitung keliling lingkaran, yaitu 2πr dan πd, di mana π (pi) adalah konstanta matematika yang nilainya mendekati 3.14159, r adalah jari-jari lingkaran, dan d adalah diameter lingkaran. Kedua rumus ini pada dasarnya sama, karena diameter lingkaran adalah dua kali jari-jarinya (d = 2r).

Rumus keliling lingkaran menunjukkan bahwa keliling lingkaran berbanding lurus dengan jari-jari atau diameternya. Artinya, jika jari-jari atau diameter lingkaran diperbesar dua kali lipat, maka kelilingnya juga akan menjadi dua kali lipat.

Contoh penggunaan rumus: Jika sebuah lingkaran memiliki jari-jari 5 cm, maka kelilingnya adalah 2 π 5 = 10π ≈ 31.42 cm. Atau, jika sebuah lingkaran memiliki diameter 10 cm, maka kelilingnya adalah π 10 ≈ 31.42 cm. Penting untuk diingat bahwa satuan keliling selalu dalam bentuk linear (cm, m, dll.).

Aplikasi Luas dan Keliling Lingkaran dalam Kehidupan Sehari-hari

Konsep luas dan keliling lingkaran memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Berikut adalah beberapa contoh:

• Arsitektur dan Konstruksi: Menghitung luas atap kubah, menentukan panjang pagar melingkar, dan merancang taman berbentuk lingkaran.
• Teknik: Merancang roda gigi, menghitung volume pipa, dan menentukan kecepatan putaran mesin.
• Desain: Membuat logo berbentuk lingkaran, merancang perhiasan, dan mengatur tata letak elemen desain.
• Memasak: Menentukan ukuran loyang kue, menghitung jumlah adonan yang dibutuhkan untuk membuat pizza, dan memotong kue menjadi bagian yang sama besar.
• Olahraga: Menghitung jarak yang ditempuh pelari di lintasan lingkaran, menentukan luas lapangan golf, dan merancang arena balap sepeda.

Selain contoh-contoh di atas, konsep luas dan keliling lingkaran juga digunakan dalam bidang astronomi, fisika, dan matematika terapan. Pemahaman yang baik tentang konsep ini akan membantu kita memecahkan berbagai masalah praktis dan memahami fenomena alam yang melibatkan bentuk lingkaran.

Tips Mudah Mengingat Rumus Lingkaran

Mengingat rumus luas dan keliling lingkaran bisa menjadi tantangan bagi sebagian orang. Berikut adalah beberapa tips yang dapat membantu Anda mengingat rumus-rumus tersebut dengan lebih mudah:

• Gunakan Jembatan Keledai: Buatlah kalimat atau frasa yang mudah diingat dan menghubungkan elemen-elemen dalam rumus. Contoh: Luas Pi R kuadrat (untuk Luas = πr²) atau Keliling Dua Pi R (untuk Keliling = 2πr).
• Visualisasikan Lingkaran: Bayangkan lingkaran dan elemen-elemennya (jari-jari, diameter, keliling). Hubungkan visualisasi ini dengan rumus yang sesuai.
• Latih Soal Secara Rutin: Semakin sering Anda berlatih mengerjakan soal-soal yang melibatkan luas dan keliling lingkaran, semakin mudah Anda mengingat rumus-rumus tersebut.
• Pahami Konsepnya: Jangan hanya menghafal rumus, tetapi pahami juga konsep dasar di balik rumus tersebut. Dengan memahami konsepnya, Anda akan lebih mudah mengingat dan menerapkan rumus dalam berbagai situasi.
• Gunakan Aplikasi atau Kalkulator: Manfaatkan aplikasi atau kalkulator yang dapat menghitung luas dan keliling lingkaran. Ini akan membantu Anda memverifikasi jawaban Anda dan memperkuat pemahaman Anda tentang rumus-rumus tersebut.

Selain tips-tips di atas, Anda juga dapat membuat catatan kecil yang berisi rumus-rumus lingkaran dan menempelkannya di tempat yang mudah Anda lihat. Dengan konsisten menerapkan tips-tips ini, Anda akan dapat mengingat rumus luas dan keliling lingkaran dengan mudah dan percaya diri.

Soal Latihan dan Pembahasan

Untuk menguji pemahaman Anda tentang luas dan keliling lingkaran, berikut adalah beberapa soal latihan beserta pembahasannya:

1. Soal 1: Sebuah taman berbentuk lingkaran memiliki diameter 14 meter. Berapakah luas taman tersebut? Pembahasan: Jari-jari taman adalah setengah dari diameter, yaitu 7 meter. Luas taman adalah π 7² = π 49 ≈ 153.94 meter persegi.
2. Soal 2: Sebuah roda sepeda memiliki jari-jari 35 cm. Berapakah keliling roda sepeda tersebut? Pembahasan: Keliling roda sepeda adalah 2 π 35 = 70π ≈ 219.91 cm.
3. Soal 3: Sebuah lingkaran memiliki luas 314 cm². Berapakah jari-jari lingkaran tersebut? Pembahasan: Luas lingkaran adalah πr² = 314. Maka, r² = 314 / π ≈ 100. Sehingga, r = √100 = 10 cm.
4. Soal 4: Sebuah lingkaran memiliki keliling 62.8 cm. Berapakah diameter lingkaran tersebut? Pembahasan: Keliling lingkaran adalah πd = 62.8. Maka, d = 62.8 / π ≈ 20 cm.
5. Soal 5: Sebuah pizza berbentuk lingkaran dipotong menjadi 8 bagian yang sama besar. Jika diameter pizza adalah 30 cm, berapakah luas setiap potongan pizza? Pembahasan: Jari-jari pizza adalah setengah dari diameter, yaitu 15 cm. Luas pizza adalah π 15² = π 225 ≈ 706.86 cm². Luas setiap potongan pizza adalah 706.86 / 8 ≈ 88.36 cm².

Dengan mengerjakan soal-soal latihan ini, Anda dapat mengasah kemampuan Anda dalam menghitung luas dan keliling lingkaran. Jangan ragu untuk mencari soal-soal latihan lainnya dan berlatih secara rutin untuk meningkatkan pemahaman Anda.

Kesimpulan

Memahami konsep luas dan keliling lingkaran adalah keterampilan matematika yang penting dan berguna dalam berbagai aspek kehidupan. Dengan memahami elemen-elemen dasar lingkaran, rumus-rumus yang relevan, dan aplikasinya dalam kehidupan sehari-hari, Anda dapat memecahkan berbagai masalah praktis dan memahami fenomena alam yang melibatkan bentuk lingkaran. Jangan lupa untuk terus berlatih dan mengasah ...